Bode Plot Screen
(Click on above image to jump to relative topic)
The Bode Plot Screen allows the measurement of a servo loop and graphs the open loop response. A Bode Plot is by far the most common means used to measure and understand the behavior of a control loop. KMotion contains advanced built-in features to allow rapid Bode Plot measurement and display. The current PID and IIR Filter transfer functions may also be superimposed and graphed.
A Bode Plot is a plot of magnitude and phase of a system with respect to frequency. Any linear system that is driven by a sinusoidal input for a long time, will output an sinusoidal signal of the same frequency. The output signal may be shifted in phase and of a different magnitude than the input. A Bode plot is a graph of both the change in phase and the relative change in magnitude (expressed in decibels, db), as a function of frequency.
A Bode plot is a useful tool used to examine the stability of a servo feedback loop. If a system has an open loop gain of -1 (magnitude of 0 db and phase of -180 degrees), then if it is placed into a negative feedback loop, it will become unstable and oscillate. Because a system's gain and phase vary as function of frequency, if the system has a magnitude of 0db and phase of -180 degrees at any frequency it will be unstable and oscillate at that frequency. The way to avoid an unstable system is to avoid having simultaneous conditions of 0db and -180 degrees occur at any frequency. Where the magnitude of the system is 0db the amount that the phase is different from -180 degrees is called the phase margin. The larger the phase margin the more stable the system. Similarly where the phase is -180 degrees the amount that the magnitude is different from 0db is called the gain margin. Again the larger the gain margin, the more stable the system. As a general rule of thumb, for a system to be reasonably stable it should have a phase margin of at least 30 degrees and a gain margin of at least 3 db.
The Bode Plot Screen attempts to identify and measure the 0 db crossover frequency (the first point where the open loop magnitude becomes less than 1, often defined as the system bandwidth, 228 Hz on the example above), the gain and phase margins, and one or two sharp peaks in the magnitude data after the crossover. Some mechanical systems have sharp resonant peaks that may cause the system to go unstable if these peaks approach the 0 db line and have phase near -180 degrees. A notch filter placed at these frequencies may increase performance. The measurements are displayed under the graph as shown below.
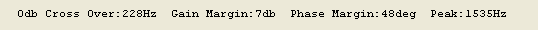
The most direct method for obtaining the open loop response, is to break the servo loop open, inject a signal into the system and measure the output. However this is usually impractical as most systems will run out of their linear range if driven in an open loop manner. KMotion operates the servo loop in its normal closed loop form, injects a command signal, measures the position response, and mathematically derives the open loop response. This does require that the servo loop function in some form as a stable closed loop servo before a measurement may be made. Performance is not a requirement so low gains might be used to obtain an initial stable system.
To perform a Bode Plot Measurement: select the channel to measure, select the desired Amplitude and Cutoff Frequency for the stimulus to be injected, select the # of samples to average, and depress the Measure Pushbutton. All current Configuration Parameters (from the Configuration Screen), Tuning Parameters (from the Step Response Screen), and Filter Parameters (from the IIR Filter Screen) will be downloaded, the selected Axis channel will be enabled, and the measurement will begin.
While the measurement is in progress the number of samples acquired will be displayed and the Measure Pushbutton will change to a Stop Pushbutton. Pushing the Stop button will stop acquiring data after the current sample is complete.
Depending on the type of plot requested (either Time Domain or Frequency Domain) either the last acquired time domain measurement will be displayed or the average all the frequency domain measurement so far acquired will be displayed.
Unfortunately Bode Plots often have regions that are very noisy. But fortunately these are almost always in regions that are not important to us. At frequencies where the open loop gain is very high (usually at low frequencies), the servo loop performs very well, and the Position closely matches the Command signal. In this case, the calculation of the Error signal (see above) is calculated by taking the difference between two nearly equal values. A small error in Position measurement will then result in a relatively large error in the calculated error value. Similarly, when the system has a very low gain (usually at high frequencies), the position signal is very small and often highly influenced by noise, or if an encoder is used, by encoder resolution. The regions of interest in order to determine system stability, are where the open loop gain is near 0db and the measurements are normally very accurate.
Additionally, instead of injecting sine waves at various frequencies individually, KMotion uses a technique where a random noise signal that is rich in many frequencies is injected. Using a method involving an FFT (Fast Fourier Transform) of the input and output, the entire frequency response may be obtained at once.
Bode Plot analysis is fundamentally based on the assumption that the system being analyzed is linear. Linear in this context means that any signal injected into a system that provides a response, might be broken into parts, each piece injected separately, and all the resulting responses when summed would equal the original response. If a system being measured does not meet this criteria then the result is basically useless and meaningless. Masses, Springs, Dampers, Inductors, Resistors, Capacitors, and all combinations thereof are examples of devices which produce very linear effects. Static friction, Saturation, and Encoder count quantization, are examples of non-linear effects.
The Bode Plot Screen allows the measurement data to be viewed in the time domain in order to check the signal amplitudes so that the optimal signal levels may be used in order to minimize the non-linear effects of saturation and quantization. Select the Plot Type drop down list shown below to switch between frequency domain and dime domain displays.
A typical time domain measurement is shown below. The blue graph shows the random stimulus to the system. The red graph shows the system's response, which in this example is the output of an encoder. Note that the position is quantized to integer counts and has a range of approximately 10 counts. This is nearly the minimum number of counts to expect a reasonable Bode Plot measurement. A larger range of encoder counts could be obtained by driving the system harder by increasing the Noise Injection Amplitude, provided there is additional output drive available.
The graphs below include the output drive signal shown in green. Note that the output drive is on the verge of saturating at the maximum allowed output value (example is from a 3 phase brushless motor, maximum allowed PWM counts of 230). This shows that we are driving the system as hard as possible without saturating in order to obtain the most accurate measurement.
Another means of improving the measurement accuracy (as well as servo performance in general) is obviously to increase the encoder resolution if economically or otherwise feasible.
Compensator Response
The Bode Plot Screen is also capable of graphing a Bode Plot of the combined PID and IIR Filters. This is often referred to as the Compensator for the system. The Cyan graph shows the magnitude of the compensator and the violet graph shows the phase of the compensator. Notice that in this example the maximum phase has been adjusted to match the 0 db crossover frequency of the system (~ 233 Hz) to maximize the system phase margin.
Axis Control
The Axis Control buttons are present to conveniently disable (Kill), Zero, or Enable an axis. If the axis becomes unstable (possible due to a gain setting too high), the Kill button may be used to disable the axis, the gain might then be reduced, and then the axis may be enabled. The Enable button downloads all parameters from all screens before enabling the axis in the same manner as the Measure button described above.
Note for brushless output modes that commutate the motor based on the current position, Zeroing the position may adversely affect the commutation.
Save/Load Data

The Save/Load Data buttons allow the captured Bode Plot to be saved to a text file and re-loaded at a later time. The text file format also allows the data to be imported into some other program for display or analysis. The file format consists of one line of header followed by one line of 9 comma separated values, one line for each frequency.
The values are:
- Frequency in Hz
- Input Stimulus - Real Part of complex number
- Input Stimulus - Complex Part of complex number (always zero)
- Measured Closed Loop Output - Real Part of complex number
- Measured Closed Loop Output - Complex Part of complex number
- Open loop Magnitude - in decibels
- Open loop Phase - in degrees
- Open loop Magnitude - in decibels - "smoothed"
- Open loop Phase - in degrees - "smoothed"
Example of data file follows:
Freq InputRe InputIm OutputRe OutputIm Mag Phase SmoothMag SmoothPhase 0 2.329706e+007 0 2.344316e+007 0 44.10739 -180 0 0 5.425347 1.968735e+007 0 1.98995e+007 -32055.19 39.34598 -171.5001 39.34598 -171.5001 10.85069 1.816919e+007 0 1.848909e+007 -713239.6 27.48402 -116.3662 29.58283 -139.1553 16.27604 2.024904e+007 0 2.124962e+007 -1383543 21.91849 -129.5997 25.14718 -134.5283 21.70139 1.53403e+007 0 1.645491e+007 -1651059 18.38331 -129.7526 22.70204 -127.6139 27.12674 1.225619e+007 0 1.301412e+007 -1336369 18.60411 -125.4229 20.60267 -123.6751 32.55208 7014539 0 7393482 -958714.3 17.18516 -118.9553 18.9778 -119.2762 . . .
Update Pushbutton

The Update button may be used to update the displayed compensator graph if any parameters (on other screens) have been modified and not downloaded or otherwise acted upon. If Measure, Download, Step, Move, Save, Close, or Enable is used on this or the any other screen then this command is unnecessary, however if none of these commands is performed, then this button may be used to update the graph.